La derivada es una herramienta fundamental en cálculo y tiene numerosas aplicaciones en diversas áreas, como:
Física y Ingeniería
- Movimiento y cinemática: La derivada se utiliza para calcular la velocidad y la aceleración de objetos en movimiento.
- Dinámica: La derivada se utiliza para calcular la fuerza y la energía de sistemas físicos.
- Electromagnetismo: La derivada se utiliza para calcular los campos eléctricos y magnéticos.
Economía
- Análisis de costos: La derivada se utiliza para calcular los costos marginales y optimizar la producción.
- Análisis de demanda: La derivada se utiliza para calcular la elasticidad de la demanda y optimizar los precios.
- Modelos de crecimiento económico: La derivada se utiliza para calcular las tasas de crecimiento y optimizar las políticas económicas.
Biología y Medicina
- Crecimiento poblacional: La derivada se utiliza para calcular las tasas de crecimiento y declive de poblaciones.
- Modelos de enfermedades: La derivada se utiliza para calcular la propagación de enfermedades y optimizar las estrategias de control.
- Farmacocinética: La derivada se utiliza para calcular la absorción, distribución, metabolismo y excreción de fármacos.
Ciencias de la Computación
- Algoritmos de optimización: La derivada se utiliza para calcular los mínimos y máximos de funciones y optimizar los algoritmos.
- Redes neuronales: La derivada se utiliza para calcular los gradientes y optimizar los pesos de las redes neuronales.
- Análisis de datos: La derivada se utiliza para calcular las tendencias y patrones en los datos.
Otros campos
- Geología: La derivada se utiliza para calcular la tasa de erosión y sedimentación.
- Climatología: La derivada se utiliza para calcular las tasas de cambio climático.
- Finanzas: La derivada se utiliza para calcular los riesgos y optimizar las inversiones.
Estos son solo algunos ejemplos de las numerosas aplicaciones de la derivada en diversas áreas. La derivada es una herramienta fundamental para analizar y optimizar sistemas complejos.
Tasa de cambio promedio e instantánea
La tasa de cambio promedio y la tasa de cambio instantánea son conceptos matemáticos que describen la variación de una función, pero en diferentes contextos. La tasa de cambio promedio se refiere al cambio promedio de una función sobre un intervalo, mientras que la tasa de cambio instantánea se refiere al cambio en un punto específico.
La tasa de cambio promedio y la tasa de cambio instantánea son conceptos fundamentales en cálculo y análisis matemático.
Tasa de cambio promedio
La tasa de cambio promedio se define como el cambio total en una función dividido por el cambio total en la variable independiente, durante un intervalo determinado. Se denota como:
Δy/Δx
Donde:
- Δy es el cambio en la función.
- Δx es el cambio en la variable independiente.
Tasa de cambio instantánea
La tasa de cambio instantánea se define como el límite de la tasa de cambio promedio cuando el intervalo se acerca a cero. Se denota como:
dy/dx
Donde:
- dy es el cambio infinitesimal en la función.
- dx es el cambio infinitesimal en la variable independiente.
La tasa de cambio instantánea se puede interpretar como la velocidad a la que cambia la función en un punto determinado.
Diferencias clave
Las principales diferencias entre la tasa de cambio promedio y la tasa de cambio instantánea son:
- La tasa de cambio promedio se calcula sobre un intervalo determinado, mientras que la tasa de cambio instantánea se calcula en un punto determinado.
- La tasa de cambio promedio es una medida de la tasa de cambio media, mientras que la tasa de cambio instantánea es una medida de la tasa de cambio en un instante determinado.
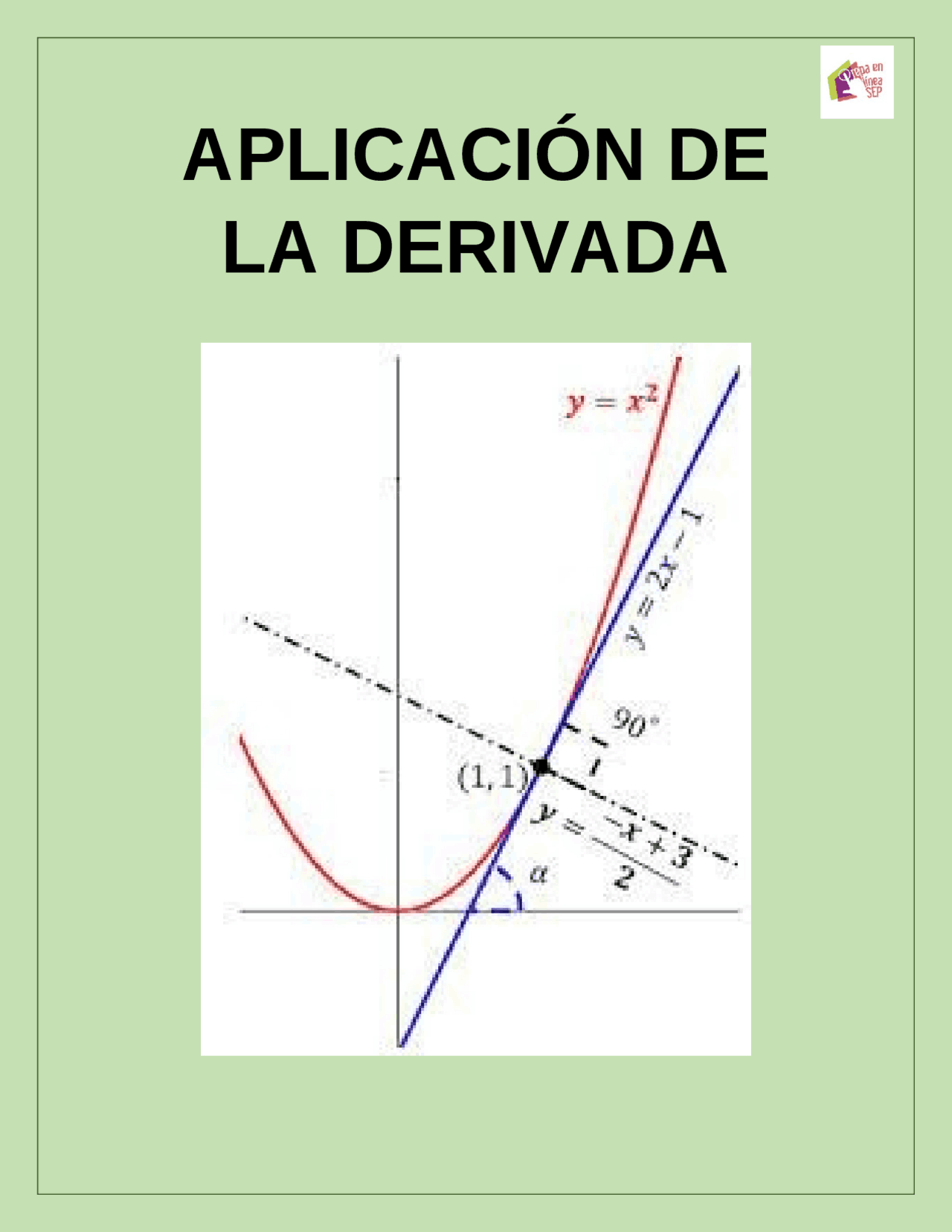
Recta tangente y normal a una curva
La recta tangente a una curva en un punto es una recta que “toca” la curva en ese punto, y su pendiente es la misma que la de la curva en ese punto. La recta normal, por otro lado, es perpendicular a la recta tangente en el punto de tangencia.
La recta tangente y la recta normal son conceptos fundamentales en geometría y cálculo.
Recta tangente
La recta tangente a una curva en un punto determinado es la recta que pasa por ese punto y tiene la misma pendiente que la curva en ese punto.
Propiedades de la recta tangente
- La recta tangente es una recta que “toca” la curva en un solo punto.
- La pendiente de la recta tangente es igual a la derivada de la función que define la curva en ese punto. Recta normal
La recta normal a una curva en un punto determinado es la recta que pasa por ese punto y es perpendicular a la recta tangente en ese punto. Propiedades de la recta normal - La recta normal es una recta que es perpendicular a la recta tangente en el punto de tangencia.
- La pendiente de la recta normal es el recíproco negativo de la pendiente de la recta tangente.
Problemas de razón de cambio
Los problemas de razón de cambio, o razones relacionadas, involucran encontrar la tasa a la que una cantidad está cambiando en relación con otra cantidad que también está cambiando. Estos problemas suelen resolverse aplicando derivadas a ecuaciones que relacionan las variables que cambian con el tiempo.
Son un tipo de problema que implica encontrar la tasa a la que cambia una cantidad con respecto a otra. Estos problemas suelen involucrar el cálculo de la derivada de una función.
Tipos de problemas de razón de cambio
- Problemas de movimiento: Estos problemas implican encontrar la velocidad o la aceleración de un objeto en movimiento.
- Problemas de crecimiento y decrecimiento: Estos problemas implican encontrar la tasa a la que cambia una cantidad, como la población de una ciudad o la cantidad de productos vendidos.
- Problemas de optimización: Estos problemas implican encontrar el máximo o mínimo de una función, como la maximización de la ganancia o la minimización del costo. Pasos para resolver problemas de razón de cambio
- Identificar la función que se quiere analizar: Debe identificar la función que describe la relación entre las variables involucradas en el problema.
- Encontrar la derivada de la función: Debe encontrar la derivada de la función para determinar la tasa de cambio de la variable dependiente con respecto a la variable independiente.
- Evaluar la derivada en el punto dado: Debe evaluar la derivada en el punto dado para encontrar la tasa de cambio en ese punto específico.
- Interpretar el resultado: Debe interpretar el resultado para responder a la pregunta del problema.
Máximos y mínimos de funciones
Son los valores más grandes (máximos) o más pequeños (mínimos) que toma la función, ya sea en un intervalo específico (locales o relativos) o en todo su dominio (globales o absolutos).
Definiciones
Máximo: Un punto en el que la función alcanza su valor más alto en un intervalo determinado.
Mínimo: Un punto en el que la función alcanza su valor más bajo en un intervalo determinado.
Tipos de máximos y mínimos
Máximo absoluto: El punto en el que la función alcanza su valor más alto en todo su dominio.
Mínimo absoluto: El punto en el que la función alcanza su valor más bajo en todo su dominio.
Máximo relativo: Un punto en el que la función alcanza un valor más alto que en los puntos cercanos.
Mínimo relativo: Un punto en el que la función alcanza un valor más bajo que en los puntos cercanos.
Criterios para determinar máximos y mínimos
Primer criterio: La derivada de la función debe ser igual a cero en el punto crítico.
Segundo criterio: La segunda derivada de la función debe ser positiva para un mínimo y negativa para un máximo.
Aplicaciones
Optimización: Los máximos y mínimos se utilizan para optimizar funciones en diversas áreas, como la economía, la ingeniería y la física.
Análisis de funciones: Los máximos y mínimos se utilizan para analizar el comportamiento de las funciones y entender sus propiedades.
Prueba de la primera derivada
En cálculo, el criterio de derivadas utiliza las derivadas de una función para ubicar sus puntos críticos y determinar si son un máximo local, un mínimo local o un punto de silla o ensilladura.
Es una técnica utilizada para determinar si una función tiene un máximo, mínimo o punto de inflexión en un punto crítico.
Pasos para aplicar la prueba de la primera derivada
- Encontrar los puntos críticos: Encontrar los puntos en los que la primera derivada de la función es igual a cero o no existe.
- Evaluar la primera derivada: Evaluar la primera derivada de la función en un intervalo alrededor de cada punto crítico.
- Determinar el signo de la primera derivada: Determinar si la primera derivada es positiva o negativa en cada intervalo.
- Interpretar los resultados: Interpretar los resultados para determinar si la función tiene un máximo, mínimo o punto de inflexión en cada punto crítico. Reglas para interpretar los resultados
- Cambio de signo de “+” a “-“: La función tiene un máximo en el punto crítico.
- Cambio de signo de “-” a “+”: La función tiene un mínimo en el punto crítico.
- No hay cambio de signo: La función tiene un punto de inflexión en el punto crítico.
Prueba de la se derivada
La prueba de la segunda derivada se usa para determinar si un punto crítico de una función es un máximo local, un mínimo local, o un punto de inflexión. Se basa en el signo de la segunda derivada en ese punto crítico. Si la segunda derivada es positiva, el punto es un mínimo local; si es negativa, es un máximo local; y si es cero, la prueba no es concluyente.
Pasos para aplicar la prueba de la segunda derivada
- Encontrar los puntos críticos: Encontrar los puntos en los que la primera derivada de la función es igual a cero o no existe.
- Evaluar la segunda derivada: Evaluar la segunda derivada de la función en cada punto crítico.
- Determinar el signo de la segunda derivada: Determinar si la segunda derivada es positiva, negativa o cero en cada punto crítico.
- Interpretar los resultados: Interpretar los resultados para determinar la naturaleza de cada punto crítico. Reglas para interpretar los resultados
- Segunda derivada positiva: La función tiene un mínimo en el punto crítico.
- Segunda derivada negativa: La función tiene un máximo en el punto crítico.
- Segunda derivada cero: La prueba es inconclusa y se debe utilizar otra técnica para determinar la naturaleza del punto crítico.
Concavidad y puntos de inflexión
La concavidad de una función describe la forma de su gráfica, si se abre hacia arriba (cóncava hacia arriba) o hacia abajo (cóncava hacia abajo). Los puntos de inflexión son los puntos donde la función cambia de concavidad, es decir, donde la gráfica pasa de ser cóncava hacia arriba a cóncava hacia abajo, o viceversa.
Concavidad
La concavidad de una función se refiere a la forma en que la función se curva. Una función puede ser:
- Concava hacia arriba: La función se curva hacia arriba, como una parábola que se abre hacia arriba.
- Concava hacia abajo: La función se curva hacia abajo, como una parábola que se abre hacia abajo. Puntos de inflexión
Un punto de inflexión es un punto en el que la concavidad de una función cambia. En un punto de inflexión: - La segunda derivada de la función es igual a cero.
- La concavidad de la función cambia de concava hacia arriba a concava hacia abajo, o viceversa. Criterios para determinar la concavidad y los puntos de inflexión
- Segunda derivada: La segunda derivada de una función puede ser utilizada para determinar la concavidad y los puntos de inflexión.
- Prueba de la segunda derivada: La prueba de la segunda derivada puede ser utilizada para determinar la concavidad y los puntos de inflexión.
Análisis de la Gráfica de una Función
El análisis de la gráfica de una función implica el estudio de diversas características que nos permiten entender su comportamiento y dibujar su representación visual. Algunos de los elementos clave a analizar son:
Dominio y Rango
El dominio es el conjunto de todos los posibles valores de entrada (x) para los que la función está definida. El rango es el conjunto de todos los posibles valores de salida (y) que la función puede tomar.
Intersecciones con los Ejes (Cortes):
Corte con el eje Y: Se encuentra haciendo x=0 en la función (f(0)).
Cortes con el eje X (Ceros o Raíces): Se encuentran haciendo f(x)=0 y resolviendo para x.
Asíntotas: Son líneas a las que la gráfica de la función se acerca infinitamente pero nunca toca (o toca en el infinito).
Asíntotas verticales: Ocurren en valores de x donde la función tiende a infinito (comúnmente cuando el denominador de una función racional es cero).
Asíntotas horizontales: Describen el comportamiento de la función cuando x tiende a infinito positivo o negativo.
Asíntotas oblicuas: Ocurren cuando el grado del numerador es exactamente uno más que el grado del denominador en una función racional.
Intervalos de Crecimiento y Decrecimiento:
Una función es creciente en un intervalo si sus valores de y aumentan a medida que x aumenta. Esto se determina cuando la primera derivada (f'(x)) es positiva.
Una función es decreciente en un intervalo si sus valores de y disminuyen a medida que x aumenta. Esto se determina cuando la primera derivada (f'(x)) es negativa.
Extremos Relativos (Máximos y Mínimos Locales): Son los puntos donde la función cambia de creciente a decreciente (máximo local) o de decreciente a creciente (mínimo local). Se encuentran buscando los puntos críticos donde f'(x) = 0 o f'(x) no existe, y luego usando el criterio de la primera o segunda derivada para clasificarlos.
Concavidad y Puntos de Inflexión: (Como se describió en el punto 4.5) Se analizan con la segunda derivada.
Simetría :
Par: Si f(-x) = f(x), la gráfica es simétrica con respecto al eje Y.
Impar : Si f(-x) = -f(x), la gráfica es simétrica con respecto al origen.
Periodicidad : Si la función repite su patrón a lo largo de un intervalo fijo.
optimizaciones derivadas
La optimización con derivadas se refiere a la aplicación de la derivada para encontrar los máximos y mínimos de una función, lo que implica encontrar los puntos críticos de la función donde la derivada es cero o no existe. Este método es útil para resolver problemas de optimización en diversas áreas, como ingeniería, economía y física.
Tipos de problemas de optimización
- Problemas de maximización: Encontrar el máximo de una función.
- Problemas de minimización: Encontrar el mínimo de una función.
Pasos para resolver problemas de optimización mediante derivadas
- Definir la función objetivo: Definir la función que se desea optimizar.
- Encontrar la derivada: Encontrar la derivada de la función objetivo.
- Encontrar los puntos críticos: Encontrar los puntos en los que la derivada es igual a cero o no existe.
- Aplicar la prueba de la segunda derivada: Aplicar la prueba de la segunda derivada para determinar si cada punto crítico es un máximo, mínimo o punto de inflexión.
- Seleccionar la solución óptima: Seleccionar la solución óptima basándose en los resultados de la prueba de la segunda derivada.
Teorema de Rolle y del Valor medio
Los teoremas de Rolle y del valor medio son resultados fundamentales en cálculo que relacionan las propiedades de una función con su derivada. El teorema de Rolle es un caso especial del teorema del valor medio, y ambos teoremas aseguran la existencia de ciertos puntos con características específicas bajo ciertas condiciones de la función.
Teorema de Rolle
El Teorema de Rolle establece que si una función f(x) es:
- Continua en el intervalo [a, b]
- Diferenciable en el intervalo (a, b)
- f(a) = f(b)
Entonces, existe al menos un punto c en el intervalo (a, b) tal que f'(c) = 0.
Teorema del Valor Medio
El Teorema del Valor Medio establece que si una función f(x) es:
- Continua en el intervalo [a, b]
- Diferenciable en el intervalo (a, b)
Entonces, existe al menos un punto c en el intervalo (a, b) tal que:
f'(c) = (f(b) – f(a)) / (b – a)
Interpretación
El Teorema de Rolle establece que si una función tiene los mismos valores en dos puntos, entonces debe tener un punto crítico entre ellos.
El Teorema del Valor Medio establece que la pendiente de la recta tangente a la función en algún punto entre a y b es igual a la pendiente de la recta secante que une los puntos (a, f(a)) y (b, f(b)).