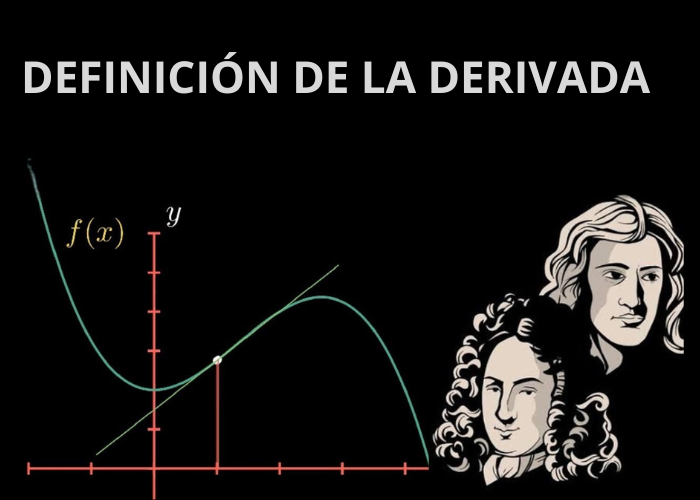
Definición de derivada como límite: La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño.
Derivacion de funciones elementales
La derivación de funciones elementales implica aplicar reglas de diferenciación para encontrar la derivada de funciones básicas como funciones polinomiales, exponenciales, logarítmicas, trigonométricas y sus combinaciones. Las reglas de diferenciación, como la regla de la potencia, la regla del producto, la regla del cociente y la regla de la cadena, son herramientas fundamentales para derivar estas funciones.
Funciones polinomiales:
La derivada de una potencia xⁿ es nxⁿ⁻¹.
Ejemplo: si f(x) = 3x², entonces f'(x) = 6x.
Funciones exponenciales:
La derivada de eˣ es eˣ.
La derivada de aˣ es aˣ * ln(a).
Ejemplo: si f(x) = 2ˣ, entonces f'(x) = 2ˣ * ln(2).
Funciones logarítmicas:
La derivada de ln(x) es 1/x.
Ejemplo: si f(x) = ln(x²), entonces f'(x) = 2/x.
Funciones trigonométricas:
La derivada de sin(x) es cos(x).
La derivada de cos(x) es -sin(x).
La derivada de tan(x) es sec²(x).
Ejemplo: si f(x) = sin(3x), entonces f'(x) = 3cos(3x).
Reglas de diferenciación:
Regla de la suma/diferencia: La derivada de una suma/diferencia de funciones es la suma/diferencia de sus derivadas. Regla del producto: La derivada de u(x)v(x) es u'(x)v(x) + u(x)v'(x).
Regla del cociente: La derivada de u(x)/v(x) es (u'(x)v(x) – u(x)v'(x))/v²(x).
Regla de la cadena: La derivada de f(g(x)) es f'(g(x)) * g'(x).
Ejemplo de aplicación:
Supongamos que f(x) = x³ * sin(x). Para derivar esta función, primero se aplica la regla del producto:
f'(x) = (3x² * sin(x)) + (x³ * cos(x)).
Posteriormente, se aplica la regla de la potencia a x³ y la derivada de sin(x) es cos(x).
regla de derivación de constante: La regla de derivación de constante establece que la derivada de una función constante es siempre cero. Esto se debe a que la pendiente de una línea horizontal (que es la gráfica de una función constante) es cero. En términos matemáticos, si f(x) = k (donde k es una constante), entonces f'(x) = 0.
Explicación:
Función constante:
Una función constante es una función que siempre devuelve el mismo valor, independientemente de la entrada. Por ejemplo, f(x) = 5 es una función constante que siempre devuelve 5.
Derivada:
La derivada de una función representa la tasa de cambio instantánea de la función en un punto dado. Geométricamente, la derivada es la pendiente de la recta tangente a la gráfica de la función en ese punto.
Pendiente de una línea horizontal:
Una línea horizontal tiene una pendiente de cero, ya que su altura no cambia con respecto a la coordenada x. Dado que la derivada representa la pendiente de la recta tangente, la derivada de una función constante, que es una línea horizontal, siempre será cero.
Regla de la potencia: La regla de potencia de las derivadas es un método de diferenciación que se utiliza cuando se necesita derivar una expresión matemática con exponente. Se utiliza cuando se nos da una expresión de la forma x n y se debe determinar su derivada. Dice: d/dx(x n ) = nx n-1 .
Regla del producto de derivadas: La regla del producto es una de las reglas de derivada que utilizamos para hallar la derivada de funciones de la forma P(x) = f(x)·g(x). La derivada de una función P(x) se denota por P'(x).

Regla del cociente:
f(x) = La función de la forma u(x)/v(x) para la cual se debe calcular la derivada. u(x) = Una función diferenciable que hace de numerador de la función f(x). u'(x) = Derivada de la función u(x). v(x) = Una función diferenciable que hace de denominador de la función dada f(x).

Regla de la cadena: La regla de la cadena permite calcular las derivadas de las funciones inversas. Si queremos calcular la derivada de y = f-1(x) escribimos f(y) = x y derivamos con respecto a x usando la regla de la cadena para obtener f/(y) · y/ = 1. Por tanto, y/ = 1/f/(y)

Derivadas de las funciones trigonometricas: La derivación de las funciones trigonométricas es el proceso matemático de encontrar el ritmo al cual una función trigonométrica cambia respecto de la variable independiente; es decir, la derivada de la función. Las funciones trigonométricas más habituales son las funciones sen(x), cos(x) y tan(x).
Derivadas de funciones exponenciales y logaritmicas: Las derivadas de las funciones exponenciales y logarítmicas son herramientas fundamentales en el cálculo. La derivada de una función exponencial con base ‘a’ es la función misma multiplicada por el logaritmo natural de la base. La derivada de una función logarítmica en base ‘a’ es 1/(x * ln(a)).
Derivadas de Funciones Exponenciales
Función exponencial general: Si f(x) = a^x, entonces f'(x) = a^x * ln(a).
Función exponencial natural (base e): Si f(x) = e^x, entonces f'(x) = e^x.
Derivadas de Funciones Logarítmicas
Función logarítmica general: Si f(x) = log_a(x), entonces f'(x) = 1 / (x * ln(a)).
Función logaritmo natural (base e): Si f(x) = ln(x), entonces f'(x) = 1/x.
derivacion implicita: La derivación implícita es un método para encontrar la derivada de una función cuando no está explícitamente despejada la variable dependiente (y) en términos de la variable independiente (x). En lugar de despejar ‘y’, se aplica la regla de la cadena y se deriva la ecuación original, considerando ‘y’ como una función de ‘x’.
En detalle:
- *
Una función implícita es una ecuación que relaciona dos o más variables sin que una de ellas esté despejada. Por ejemplo, x² + y² = 1 es una función implícita porque ‘y’ no está despejada.
- Derivación:
Se deriva cada término de la ecuación con respecto a la variable independiente (x). - Regla de la cadena:
Cuando se deriva un término que contiene ‘y’, se aplica la regla de la cadena, multiplicando el resultado de la derivada por dy/dx. - Despeje:
Finalmente, se despeja dy/dx, que representa la derivada de la función implícita.
Derivadas sucesivas : Las derivadas sucesivas se obtienen al derivar una función varias veces. La primera derivada se obtiene derivando la función original, la segunda derivada se obtiene derivando la primera derivada, y así sucesivamente.

Leave a Reply